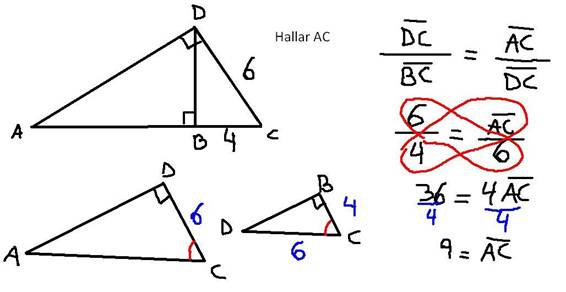
A la hora de realizar las tablas , encontraremos infinidad de teoremas y…
Propiedades de Ángulos y Arcos
Angulo Central

La relación entre un ángulo central y el arco de circunferencia comprendido se rige por:
β = Arc
Relación entre ángulo central y ángulo inscrito

La medida del ángulo inscrito es la mitad de la medida de su ángulo central correspondiente
Β = 2 α
Relación entre ángulo formado y arcos comprendidos

La relación entre el ángulo formado entre la intercepción de dos cuerdas y los arcos comprendidos esta dada por:
β = 0.5 ( Arc1 + Arc2 )
Angulo formado por cuerda-tangente

El ángulo formado por una cuerda y la recta tangente es la mitad del arco correspondiente.
2 β = Arc
Angulo exterior a la circunferencia

El ángulo exterior es igual a la mitad de la diferencia entre los arcos formados por las rectas secantes.
β = 0.5 (Arc2 – Arc1 )
Intersección de Cuerdas

El producto de los segmentos de una cuerda es igual al producto de los segmentos de la otra cuerda.
a × c= b × d
Intersección de Secantes

El producto de una secante y su parte exterior, es igual al producto de la otra secante y su parte exterior.
b × a = c × d
Intersección entre Secante y Tangente

El producto de la secante y su parte exterior es igual al cuadrado de la tangente.
A2 = b × c